목차
- B-Tree 란
- B-Tree 개념
- B-Tree 특징
- B-Tree의 동작
- B-Tree의 시간 복잡도
- B-Tree 활용 사례
- B+Tree란?
B-트리(B-Tree)란?
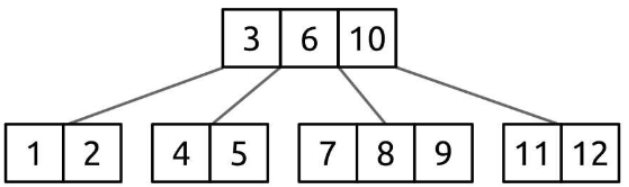
B-트리(B-Tree)는 균형 잡힌 트리 자료구조로, 특히 데이터베이스나 파일 시스템에서 대용량 데이터를 효율적으로 저장하고 관리하기 위해 고안된 트리이다. 이진 트리와 달리, B-트리는 각 노드가 여러 개의 자식 노드와 여러 개의 키를 가질 수 있는 구조이다.
이 때문에 높이를 낮게 유지하여, 빠른 검색과 삽입, 삭제 연산이 가능하다.
B-트리의 주요 개념
M-차 B-트리:
- B-트리의 차수(M)는 각 노드가 가질 수 있는 최대 자식 노드의 수를 나타낸다.
- 예를 들어, 3차 B-트리는 각 노드가 최대 3개의 자식을 가질 수 있다.
노드의 키 개수
- 각 노드는 최소 ⌈M/2⌉-1(반 올림)개의 키와 최대 M-1개의 키를 저장할 수 있다.
- 루트 노드는 예외적으로 하나 이상의 키를 가질 수 있다.
- 노드가 자녀가 x개를 가졌다면 key는 x-1개를 가질 수 있다.
균형 잡힌 트리
- B-트리는 모든 리프 노드가 같은 깊이에 위치하도록 트리의 균형을 유지한다.
- 삽입이나 삭제 시 균형을 유지하기 위해 노드를 분할하거나 병합할 수 있다.
자녀 노드의 수
- 부모 노드의 key 수가 x개라면 자녀 노드의 최대 수는 언제나 x+1개이다.
- 노드가 최소 하나의 key는 가지기 때문에 M차 B-트리 인지와 상관없이 부모 노드는 최소 두 개의 자녀는 가진다.
- M이 정해지면 root 노드를 제외한 부모 노드는 최소 ⌈M/2⌉ 개의 자녀 노드를 가질 수 있게 된다.(root node, leaf node 제외)
B-트리의 특징
균형 유지
- 삽입, 삭제 연산 후에도 모든 리프 노드들은 같은 레벨에 있다.
- 그렇기 때문에 트리는 언제나 균형을 유지하여 트리의 높이를 일정하게 유지한다.
- 이는 모든 연산의 시간 복잡도를 O(log n)으로 보장한다.
다수의 자식 노드
- 각 노드는 여러 자식 노드를 가질 수 있어 트리의 높이가 낮아지며, 이로 인해 대규모 데이터를 효율적으로 처리할 수 있다.
디스크 I/O 최적화
- 한 번의 디스크 접근으로 여러 데이터를 읽을 수 있어 디스크 I/O를 최소화하도록 설계되었다.
B-트리의 동작
B-트리의 데이터 삽입
- 추가는 항상 리프 노드에서 발생한다.
- 노드가 넘치면 가운데(median) key를 기준으로 좌우 key들은 분할하고 가운데 key는 승진한다.
- 노드가 넘친다는 것은 각 노드가 가질 수 있는 최대 key의 수 (M-1) 개를 넘었을 때이다.
- 추가를 할때 데이터가 오름차순으로 정렬한 형태에서 저장을 해줘야 한다.
B-트리의 데이터 삭제
- 삭제도 항상 리프 노드에서 발생
- 삭제 후 최소 key 수보다 적어졌다면 재조정한다.
- ⌈M/2⌉ - 1: B-tree에서 각 노드의 최소 key수(root node 제외)
- internal 노드 데이터 삭제: 리프 노드에 있는 데이터와 위치를 바꾼 후 삭제한다.
- 삭제할 데이터의 선임자나 후임자와 위치를 바꿔준다.
재조정 방법
- 최소 key 수보다 적어졌다면 key수가 여유있는 형제의 지원을 받는다.
- 1번이 불가능하면 부모의 지원을 받고 형제와 합친다.
- 2번 후 부모에 문제가 있다면 거기서 다시 재조정한다.
B-트리의 시간 복잡도
| 연산 | 시간 복잡도 | 설명 |
| 삽입 | O(log n) | 삽입된 키를 적절한 위치에 배치하고 필요한 경우 노드를 분할한다. |
| 삭제 | O(log n) | 삭제 후 트리의 균형을 유지하며, 병합이나 키 대여가 일어난다. |
| 검색 | O(log n) | 트리의 높이에 비례하여 키를 탐색한다. |
B-트리의 활용 사례
- 데이터베이스 인덱스: B-트리는 대규모 데이터를 빠르게 검색할 수 있는 인덱스 구조로 많이 사용된다.
- 파일 시스템: B-트리는 디렉토리 구조와 파일 레이아웃을 관리하는 데 자주 활용된다.
B+ 트리(B+ Tree)란?
B+ 트리는 B-트리의 변형된 버전으로, 데이터베이스 시스템과 파일 시스템에서 주로 사용되는 트리 자료구조이다.
B+ 트리는 B-트리와 달리 모든 실제 데이터가 리프 노드에만 저장되며, 내부 노드는 오직 인덱스 역할만을 수행한다.
B+ 트리의 특징
- 모든 데이터는 리프 노드에만 저장: B+ 트리의 데이터는 리프 노드에만 위치하며, 내부 노드는 인덱스 역할을 한다. 이는 일관성 있는 검색 성능을 보장한다.
- 리프 노드의 연결성: 리프 노드는 서로 연결되어 있어, 순차적으로 데이터를 조회할 수 있다. 이로 인해 범위 검색이 용이해진다.
- 균형 유지: 삽입과 삭제 후에도 트리는 자동으로 균형을 유지하며, 모든 리프 노드는 동일한 깊이에 위치하게 된다.
B+ 트리의 구조
- 루트 노드: 트리의 최상위 노드로, 전체 트리의 시작점이다.
- 내부 노드: 루트와 리프 노드 사이의 노드들로, 인덱스 역할만 수행한다. 데이터를 저장하지 않는다.
- 리프 노드: 모든 데이터가 저장된 노드들로, 검색 연산에서 최종적으로 탐색되는 노드이다. 각 리프 노드는 다음 리프 노드를 가리키는 포인터를 갖는다.
B+ 트리의 시간 복잡도
| 연산 | 시간 복잡도 | 설명 |
| 삽입 | O(log n) | 리프 노드에 삽입하며, 분할이 필요할 때 상위 노드로 중간 값을 올린다. |
| 삭제 | O(log n) | 리프 노드에서 삭제하며, 균형이 깨지면 병합을 수행한다. |
| 검색 | O(log n) | 내부 노드를 통해 빠르게 리프 노드로 접근하여 검색한다. |
'자료구조' 카테고리의 다른 글
| [자료구조] 힙 (0) | 2024.11.24 |
|---|---|
| [자료구조] Set과 Hash set (1) | 2024.10.25 |
| [자료구조] Red-Black 트리 (1) | 2024.10.25 |
| [자료구조] AVL 트리 (0) | 2024.10.24 |
| [자료구조] 이진 탐색 트리 (0) | 2024.10.23 |


