배열(Array)과 리스트(ArrayList, LinkedList)는 데이터 구조에서 매우 중요한 역할을 한다.
각각의 데이터 구조는 메모리 관리 방식과 시간 복잡도가 다르기 때문에, 적절한 상황에 맞게 선택하는 것이 중요하다.
배열의 메모리 관리와 주소 참조, 그리고 ArrayList와 LinkedList의 개념, 각 연산의 시간 복잡도, 장단점에 대해 설명하겠다.
먼저 자료 구조의 가장 기본이 되는 배열의 특징을 알아보자.
배열(Array)
배열은 같은 타입의 데이터가 연속적인 메모리 공간에 저장되는 자료 구조이다.
각 요소는 인덱스를 사용해 빠르게 접근할 수 있으며, 고정된 크기를 가지는 데이터 구조이다.
배열의 특징1 - 배열과 인덱스
1. 연속된 메모리 공간 할당

- 배열은 메모리에서 연속된 공간을 할당받는다.
- 즉, 배열의 첫 번째 요소의 주소값에 고정된 간격(각 요소의 크기만큼)을 더해 나가면 나머지 요소들의 메모리 주소를 구할 수 있다.
예시)
- 예: 배열이 int 타입(4바이트)을 저장하는 경우, 배열의 첫 번째 요소가 x100번지에 저장되면 두 번째 요소는 x104번지에, 세 번째 요소는 x108번지에 저장된다.
2. 인덱스를 사용한 빠른 접근
arr[2] 에 위치한 자료를 찾는다고 가정

- 배열은 메모리상에 순서대로 붙어서 존재한다.
- int 는 4byte 를 차지한다.
- 따라서 배열의 시작 위치인 x100 부터 시작해서 자료의 크기(4byte)와 인덱스 번호를 곱하면 원하는 메모리 위치를 찾을 수 있다.
- 배열의 시작 참조(x100) + (자료의 크기(4byte) * 인덱스 위치(2)) = x108이 나온다. 여기에는 숫자 10이 들어있다.
3. 메모리 참조 주소 관점
- 공식: 배열의 시작 참조 + (자료의 크기 * 인덱스 위치)
- arr[0]: x100 + (4byte * 0): x100
- arr[1]: x100 + (4byte * 1): x104
- arr[2]: x100 + (4byte * 2): x108
- 조회 연산의 시간 복잡도는 O(1)
장점
- 배열의 경우 인덱스를 사용하면 한번의 계산으로 매우 효율적으로 자료의 위치를 찾을 수 있다.
- 인덱스를 통한 입력, 변경, 조회 모두 한번의 계산으로 필요한 위치를 찾아서 처리할 수 있다.
- 정리하면 배열에서 인덱스를 사용하는 경우 데이터가 아무리 많아도 한 번의 연산으로 필요한 위치를 찾을 수 있다.
단점
- 배열이 연속된 메모리 공간을 차지하기 때문에 가능한 방식이며, 빠른 데이터 접근이 가능하다.
- 하지만 배열의 크기를 미리 지정해야 하고, 크기 변경이 불가능하다는 단점이 있다.
배열의 특징2 - 배열의 검색
배열에 들어있는 데이터를 찾는 것을 검색이라 한다.
배열에 들어있는 데이터를 검색할 때는 배열에 들어있는 데이터를 하나하나 비교해야 한다.
이때는 이전과 같이 인덱스를 사용해서 한번에 찾을 수 없다.
대신에 배열안에 들어있는 데이터를 하나하나 확인해야 한다.
따라서 평균적으로 볼때 배열의 크기가 클 수록 오랜 시간이 걸린다.
배열의 크기와 검색 연산
- 배열의 크기 1: arr[0] ➔ 연산 1회
- 배열의 크기 2: arr[0], arr[1] ➔ 연산 2회
- 배열의 크기 3: arr[0], arr[1], arr[2] ➔ 연산 3회
- 배열의 크기 10: arr[0], arr[1], arr[2] ... arr[9] ➔ 연산 10회
- 배열의 크기 1000: arr[0], arr[1], arr[2] ... arr[999] ➔ 연산 1000회
배열의 순차 검색은 배열에 들어있는 데이터의 크기 만큼 연산이 필요하다.
배열의 크기가 n이면 연산도 n만큼 필요하다.
배열의 특징3 - 데이터 추가
이번에는 배열의 특정 위치에 데이터를 추가해보자.
추가는 기존 데이터를 유지하면서 새로운 데이터를 입력하는 것을 뜻한다. 참고로 데이터를 중간에 추가하면 기존 데이
터가 오른쪽으로 한 칸씩 이동해야 한다. 이 말을 좀 더 쉽게 풀어보자면 데이터를 추가하려면 새로운 데이터를 입력할
공간을 확보해야 한다. 따라서 기존 데이터를 오른쪽으로 한 칸씩 밀어야 한다. (기존 데이터의 인덱스를 하나씩 증가시
켜야 한다.)
배열의 위치에 따른 데이터 추가 예시
- 1. 배열의 첫번째 위치에 추가
- 2. 배열의 중간 위치에 추가
- 3. 배열의 마지막 위치에 추가
배열의 첫번째 위치에 추가

- 배열의 첫번째 위치에 숫자 3을 추가하는 경우

- 기존 데이터들을 모두 오른쪽으로 한 칸씩 밀어서 추가할 위치를 확보해야 한다.
- 이때 배열의 마지막 부분 부터 오른쪽으로 밀어야 데이터를 유지할 수 있다.
- 왼쪽의 데이터를 오른쪽에 대입하는 과정을 반복한다.
배열의 중간 위치에 추가
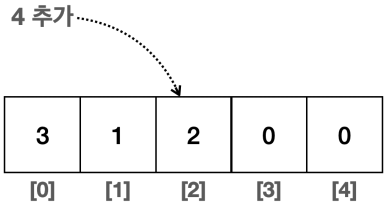
- 배열의 중간이나 특정 index 위치에 추가하는 경우
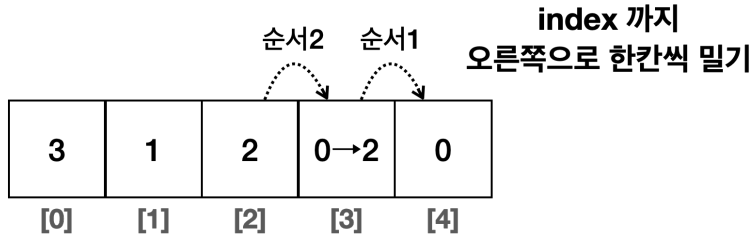
- 지정한 index에 데이터를 추가할 위치를 확보해야 한다.
- 따라서 index부터 시작해서 데이터들을 오른쪽으로 한 칸씩 밀어야 한다.
- 이 경우 index 왼쪽의 데이터는 이동하지 않아도 된다.
배열의 마지막 위치에 추가
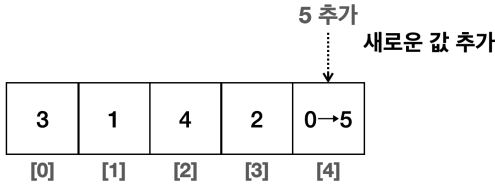
- 배열의 마지막 위치에 데이터를 추가하는 경우 여기가 배열의 마지막이다.
- 이 경우 기존 데이터를 이동하지 않아도 된다. 따라서 단순하게 값만 입력하면 된다.
배열에 데이터를 추가할 때 위치에 따른 성능 변화
1. 배열의 첫번째 위치에 추가
- 배열의 첫번째 위치를 찾는데는 인덱스를 사용하므로 O(1)이 걸린다.
- 모든 데이터를 배열의 크기만큼 한 칸씩 이동해야 한다. 따라서 O(n) 만큼의 연산이 걸린다.
- O(1 + n) O(n)이 된다.
2. 배열의 중간 위치에 추가
- 배열의 위치를 찾는데는 O(1)이 걸린다.
- index의 오른쪽에 있는 데이터를 모두 한 칸씩 이동해야 한다. 따라서 평균 연산은 O(n/2)이 된다.
- O(1 + n/2) O(n)이 된다.
3. 배열의 마지막 위치에 추가
- 이 경우 배열이 이동하지 않고 배열의 길이를 사용하면 마지막 인덱스에 바로 접근할 수 있으므로 한번의 계산으로 위치를 찾을 수 있고, 기존 배열을 이동하지 않으므로 O(1)이 된다.
코드 예시)
public class ArrayMain2 {
public static void main(String[] args) {
int[] arr = new int[5];
arr[0] = 1;
arr[1] = 2;
// 배열의 초기 상태
System.out.println("배열의 초기 상태");
System.out.println(Arrays.toString(arr));
// 배열의 첫번째 위치에 추가
// 기본 배열의 데이터를 한 칸씩 뒤로 밀고 첫번째 위치에 추가
System.out.println("배열의 첫번째 위치에 3추가 O(n)");
addFirst(arr, 3);
System.out.println(Arrays.toString(arr));
// 인덱스 위치에 추가
// 기본 배열의 데이터를 한 칸씩 밀고 배열의 인덱스 위치에 추가
System.out.println("배열의 index(2) 위치에 4 추가 O(n)");
addAtIndex(arr, 2, 4);
System.out.println(Arrays.toString(arr));
// 배열의 마지막 위치에 추가
System.out.println("배열의 마지막 위치에 5 추가 O(1)");
addLast(arr, 5);
System.out.println(Arrays.toString(arr));
}
private static void addFirst(int[] arr, int newValue) {
for (int i = arr.length - 1; i > 0; i--) {
arr[i] = arr[i - 1];
}
arr[0] = newValue;
}
private static void addAtIndex(int[] arr, int index, int newValue) {
for (int i = arr.length - 1; i > index; i--) {
arr[i] = arr[i - 1];
}
arr[index] = newValue;
}
private static void addLast(int[] arr, int newValue) {
arr[arr.length - 1] = newValue;
}
}배열의 초기 상태
[1, 2, 0, 0, 0]
배열의 첫번째 위치에 3 추가 O(n)
[3, 1, 2, 0, 0]
배열의 index(2) 위치에 4 추가 O(n)
[3, 1, 4, 2, 0]
배열의 마지막 위치에 5 추가 O(1)
[3, 1, 4, 2, 5]배열의 한계
배열은 가장 기본적인 자료 구조이고, 특히 인덱스를 사용할 때 최고의 효율이 나온다.
하지만 이런 배열에는 큰 단점이 있다. 바로 배열의 크기를 배열을 생성하는 시점에 미리 정해야 한다는 점이다.
예를 들어서 이벤트를 하는데, 누구나 이벤트에 참여할 수 있고, 이벤트가 끝나면 추첨을 통해서 당첨자를 정한다고 가정해보자.
이때 이벤트에 참여하는 사용자를 배열에 보관한다고 가정하자. 사용자들은 실시간으로 계속 추가된다. 이때 넉넉하게 길이가 1000인 배열을 사용했는데, 예상보다 이벤트 참여자가 많아서 1000명을 넘게 된다면 더 많은 사용자가 이벤트에 참여하지 못하는 문제가 발생한다. 그렇다고 처음부터 너무 많은 배열을 확보하면 메모리가 많이 낭비된다. 배열처럼 처음부터 정적으로 길이가 정해져있는 것이 아니라, 동적으로 언제든지 길이를 늘리고 줄일 수 있는 자료 구조가 있다면 편리할 것이다.
'자료구조' 카테고리의 다른 글
| [자료구조] 스택과 큐 (0) | 2024.10.11 |
|---|---|
| [자료구조] 배열 리스트, 연결 리스트 (4) | 2024.10.08 |
| [자료구조] 시간복잡도와 공간복잡도 (0) | 2024.10.07 |
| [자료구조] 비트(Bit), 바이트(byte), 자료형의 종류 (0) | 2024.10.06 |
| [자료구조] 자료구조와 알고리즘이란? (0) | 2024.10.06 |



